Applied Information Economics (AIE)
Applied Information Economics (AIE) is a scientific and theoretical method developed for addressing the dilemmas even when it may seem like there is no way to measure the problem, such as with economic value. Applied Information Economics uses methods that show independently, scientifically measured improvements to management forecasts and decisions. Concepts that seemed like intangibles, now have proven economic formulae to help your business drive results.[1]
Applied Information Economics Definition.[2]
Applied information economics (AIE) is a decision analysis method developed by Douglas W. Hubbard and partially described in his book How to Measure Anything: Finding the Value of Intangibles in Business (2007; 2nd ed. 2010; 3rd ed. 2014). AIE is a method for the practical application of several proven methods from decision theory and risk analysis including the use of Monte Carlo methods. However, unlike some other modeling approaches with simulations, AIE incorporates the following:
- Calibrated Probability Assessment - This is a method for training estimators and experts (who are relied on for the inputs in Monte Carlo methods) to be neutrally confident about their assigned probabilities. That is, their probabilities are neither overconfident (too high) nor underconfident (too low).
- Computing the value of additional information. AIE uses information value calculations from decision theory such as the expected value of perfect information and the value of imperfect (partial) information. Often, this is done for a large number of uncertain variables in some type of decision model or business case. The result will reveal where efforts to reduce uncertainty by making further measurements are best spent.
- Empirical Methods applied according to the information value of the measurement. This step is, in fact, the reason for the name of the method. Most Monte Carlo modeling experts stop modeling after the first (uncalibrated) probability estimates from experts and there is usually little emphasis on further measurements with empirical methods. Since AIE computes the value of additional information, measurement can be selective and focused. This step often results in a very different set of measurement priorities than would otherwise have been used
- Various optimization methods including Modern Portfolio Theory (MPT) and other methods are applied to determine ideal risk and return positions for a set of alternatives.
Practitioners of AIE claim that if something affects an organization, it must be observable and, therefore, measurable
Applied Information Economics Methodology[3]
Applied Information Economics (AIE) is a unique methodology to rigorously apply a specialized economic theory to the problems confronting the executive in charge of the “IT portfolio.” AIE is a synthesis of techniques from a variety of scientific and mathematical fields. The tools of economics, financial theory, and statistics are all major contributors to AIE. But in addition to these more familiar fields AIE includes Decision Theory - the formulation of decisions into a mathematical framework - and Information Theory - the mathematical modeling of transmitting and receiving information. It is important to emphasize, however, that even though AIE is a theoretically well-founded set of techniques, it is a very practical approach. Every proper application of AIE keeps the bottom line squarely in mind. All output from the AIE project is in support of specific practical business objectives. The powerful techniques of AIE clarify, measure, and provide optimal recommendations for a variety of situations. AIE applies across the enterprise to solve some of its most perplexing problems, including the following:
- Using mathematical models to improve cost/benefit analysis (CBA) for better decisions at all levels of IT
- Developing financially-based quality assurance measurements to insure that the implementation of IT decisions are effective
- Developing a strategic plan for information systems based on identifying the best opportunities for economic contribution by information systems
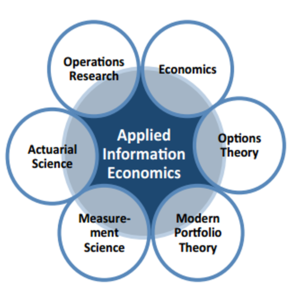
source: Hubbard Research
The Four Phases of Applied Information Economics (AIE)[4]
Hubbard lays out the application of AIE in four phases (0 – 3).
- Phase 0 is a preparation phase which includes identifying workshop participants, developing the first cut of the measurement questions and then assigning the workshop participants pre-reading (homework) based on those initial questions. Maximizing the value of the workshops requires priming the participants with homework. The homework makes sure everyone is prepared for the workshops so that time is note wasted having coming up to speed. This also helps to reset any organizational anchor bias.
- Phase 1: Hold workshop(s) for problem definition, building a decision model, and developing initially calibrated estimates. Calibration exercises aid participants so they can quantify the initial variables as a range at a 90% confidence interval or as a probability distribution, rather than a single number.
- Phase 2: This phase focuses on analyzing the value of information, the first cut at the measurement methods, refining the measurement methods, updating the decision model and then re-running the value of information analysis to make sure we don’t have to change the measurement approach . Hubbard points out (and my experience attests) that during this step, you often determine that most variables have sufficient certainty, so the organization needs to do no further measurement beyond the calibrated estimate. This step ensures that the variables that move forward in the measurement process add value.
- Phase 3: Use the data to make the decision(s) to run a Monte Carlo analysis to refine any of the metrics procedures needed, use the data to make the decisions identified and generate a final report and presentation (even Hubbard is a consultant, thus, a presentation).
The Five Steps of Applied Information Economics (AIE)[5]
The following are the five steps of Applied Information Economics (AIE):
- Define a decision problem and the relevant variables. (Start with the decision you need to make, then figure out which variables would make your decision easier if you had better estimates of their values.): Hubbard illustrates this step by telling the story of how he helped the Department of Veterans Affairs (VA) with a measurement problem. The VA was considering seven proposed IT security projects. They wanted to know “which… of the proposed investments were justified and, after they were implemented, whether improvements in security justified further investment…” Hubbard asked his standard questions: “What do you mean by ‘IT security’? Why does it matter to you? What are you observing when you observe improved IT security?” It became clear that nobody at the VA had thought about the details of what “IT security” meant to them. But after Hubbard’s probing, it became clear that by “IT security” they meant a reduction in the frequency and severity of some undesirable events: agency-wide virus attacks, unauthorized system access (external or internal),unauthorized physical access, and disasters affecting the IT infrastructure (fire, flood, etc.) And each undesirable event was on the list because of specific costs associated with it: productivity losses from virus attacks, legal liability from unauthorized system access, etc. Now that the VA knew what they meant by “IT security,” they could measure specific variables, such as the number of virus attacks per year.
- Determine what you know. (Quantify your uncertainty about those variables in terms of ranges and probabilities.): The next step is to determine your level of uncertainty about the variables you want to measure. To do this, you can express a “confidence interval” (CI). A 90% CI is a range of values that is 90% likely to contain the correct value. For example, the security experts at the VA were 90% confident that each agency-wide virus attack would affect between 25,000 and 65,000 people. Unfortunately, few people are well-calibrated estimators. For example in some studies, the true value lay in subjects’ 90% CIs only 50% of the time! These subjects were overconfident. For a well-calibrated estimator, the true value will lie in her 90% CI roughly 90% of the time. His first technique is the equivalent bet test. Suppose you’re asked to give a 90% CI for the year in which Newton published the universal laws of gravitation, and you can win $1,000 in one of two ways:
- You win $1,000 if the true year of publication falls within your 90% CI. Otherwise, you win nothing.
- You spin a dial divided into two “pie slices,” one covering 10% of the dial, and the other covering 90%. If the dial lands on the small slice, you win nothing. If it lands on the big slice, you win $1,000.
Hubbard’s second method for improving calibration is simply repetition and feedback. Make lots of estimates and then see how well you did. For this, play CFAR’s Calibration Game. Hubbard also asks people to identify reasons why a particular estimate might be right, and why it might be wrong. He also asks people to look more closely at each bound (upper and lower) on their estimated range. A 90% CI “means there is a 5% chance the true value could be greater than the upper bound, and a 5% chance it could be less than the lower bound. This means the estimators must be 95% sure that the true value is less than the upper bound. If they are not that certain, they should increase the upper bound… A similar test is applied to the lower bound.”
- Pick a variable, and compute the value of additional information for that variable. (Repeat until you find a variable with reasonably high information value. If no remaining variables have enough information value to justify the cost of measuring them, skip to step 5.): Information can have three kinds of value:
- Information can affect people’s behavior (e.g. common knowledge of germs affects sanitation behavior).
- Information can have its own market value (e.g. you can sell a book with useful information).
- Information can reduce uncertainty about important decisions. (This is what we’re focusing on here.)
When you’re uncertain about a decision, this means there’s a chance you’ll make a non-optimal choice. The cost of a “wrong” decision is the difference between the wrong choice and the choice you would have made with perfect information. But it’s too costly to acquire perfect information, so instead we’d like to know which decision-relevant variables are the most valuable to measure more precisely, so we can decide which measurements to make.
- Apply the relevant measurement instrument(s) to the high-information-value variable. (Then go back to step 3.): If you followed the first three steps, then you’ve defined a variable you want to measure in terms of the decision it affects and how you observe it, you’ve quantified your uncertainty about it, and you’ve calculated the value of gaining additional information about it. Now it’s time to reduce your uncertainty about the variable – that is, to measure it. Each scientific discipline has its own specialized measurement methods. Hubbard’s book describes measurement methods that are often useful for reducing our uncertainty about the “softer” topics often encountered by decision-makers in business. To figure out which category of measurement methods are appropriate for a particular case, we must ask several questions:
- Decomposition: Which parts of the thing are we uncertain about?
- Secondary research: How has the thing (or its parts) been measured by others?
- Observation: How do the identified observables lend themselves to measurement?
- Measure just enough: How much do we need to measure it?
- Consider the error: How might our observations be misleading?
- Make a decision and act on it. (When you’ve done as much uncertainty reduction as is economically justified, it’s time to act!): The last step will make more sense if we first “bring the pieces together.” Hubbard now organizes his consulting work with a firm into 3 phases. (4 phases counting Phase 0 which is the preparation phase)
- Phase 0: Project Preparation
- Initial research: Interviews and secondary research to get familiar on the nature of the decision problem.
- Expert identification: Usually 4–5 experts who provide estimates.
- Phase 1: Decision Modeling
- Decision problem definition: Experts define the problem they’re trying to analyze.
- Decision model detail: Using an Excel spreadsheet, the AIE analyst elicits from the experts all the factors that matter for the decision being analyzed: costs and benefits, ROI, etc.
- Initial calibrated estimates: First, the experts undergo calibration training. Then, they fill in the values (as 90% CIs or other probability distributions) for the variables in the decision model.
- Phase 2: Optimal measurements
- Value of information analysis: Using Excel macros, the AIE analyst runs a value of information analysis on every variable in the model.
- Preliminary measurement method designs: Focusing on the few variables with highest information value, the AIE analyst chooses measurement methods that should reduce uncertainty.
- Measurement methods: Decomposition, random sampling, Bayesian inversion, controlled experiments, and other methods are used (as appropriate) to reduce the uncertainty of the high-VoI variables.
- Updated decision model: The AIE analyst updates the decision model based on the results of the measurements.
- Final value of information analysis: The AIE analyst runs a VoI analysis on each variable again. As long as this analysis shows information value much greater than the cost of measurement for some variables, measurement and VoI analysis continues in multiple iterations. Usually, though, only one or two iterations are needed before the VoI analysis shows that no further measurements are justified.
- Phase 3: Decision optimization and the final recommendation
- Completed risk/return analysis: A final MC simulation shows the likelihood of possible outcomes.
- Identified metrics procedures: Procedures are put in place to measure some variables (e.g. about project progress or external factors) continually.
- Decision optimization: The final business decision recommendation is made (this is rarely a simple “yes/no” answer).
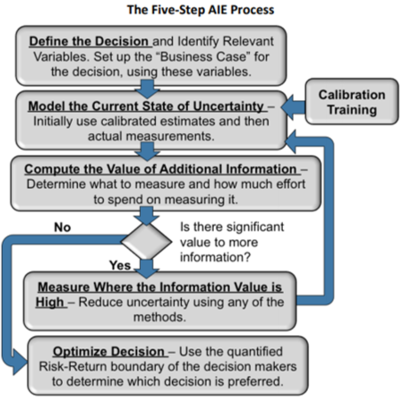
source: Hubbard Research
Applied Information Economics Certification[6]
The National Association of Business Economics (NABE) is the premier source for high-quality continuing education in the field of economics, offering a portfolio of courses with an emphasis on practice over theory. Through the Certified Business Economist (CBE) program, NABE expands and formalizes this content as a unified, comprehensive body of knowledge. The CBE designation is earned by demonstrating mastery of this body of knowledge.[7]
Hubbard Decision Research (HDR) has a structured business analyst certification program to get you qualified to use the Applied Information Economics theory on your own. By becoming certified in Applied Information Economics (AIE), you and your team will qualify in assisting, managing, and supervising the risk/return analysis projects and the Applied Information Economics implementation projects for your business.
See Also
References
- ↑ What is Applied Information Economics (AIE)?-Hubbard Decision Research
- ↑ Applied Information Economics Definition -Wikipedia
- ↑ Applied Information Economics:A New Method for Quantifying IT Value -Hubbard
- ↑ What are the Four Phases of Applied Information Economics (AIE)? -TCagley
- ↑ What are the Five Steps of Applied Information Economics (AIE)? -LessWrong
- ↑ AIE Certification-Hubbard Research Training
- ↑ The Certification in Applied Economics and Data Analytics
Further Reading
- How to Measure Anything: Finding the Value of Intangibles in Business -Hubbard Research
- Modeling Resilience with Applied Information Economics -Doug Hubbard and Matt Millar
- Regarding the Applied Information Economics Methodology -Federal CIO Council
- A Case Study of the Applied Information Economics Methodology For an Infrastructure IT Investment -DFID UK
