Abstract Data Type
In computer science, an Abstract Data Type (ADT) is a mathematical model for data types. An abstract data type is defined by its behavior (semantics) from the point of view of a user, of the data, specifically in terms of possible values, possible operations on data of this type, and the behavior of these operations. This mathematical model contrasts with data structures, which are concrete representations of data, and are the point of view of an implementer, not a user.
Formally, an ADT may be defined as a "class of objects whose logical behavior is defined by a set of values and a set of operations"; this is analogous to an algebraic structure in mathematics. What is meant by "behavior" varies by author, with the two main types of formal specifications for behavior being axiomatic (algebraic) specification and an abstract model; these correspond to axiomatic semantics and operational semantics of an abstract machine, respectively. Some authors also include the computational complexity ("cost"), both in terms of time (for computing operations) and space (for representing values). In practice many common data types are not ADTs, as the abstraction is not perfect, and users must be aware of issues like arithmetic overflow that are due to the representation. For example, integers are often stored as fixed-width values (32-bit or 64-bit binary numbers), and thus experience integer overflow if the maximum value is exceeded.
ADTs are a theoretical concept, in computer science, used in the design and analysis of algorithms, data structures, and software systems, and do not correspond to specific features of computer languages—mainstream computer languages do not directly support formally specified ADTs. However, various language features correspond to certain aspects of ADTs, and are easily confused with ADTs proper; these include abstract types, opaque data types, protocols, and design by contract. ADTs were first proposed by Barbara Liskov and Stephen N. Zilles in 1974, as part of the development of the CLU language.[1]
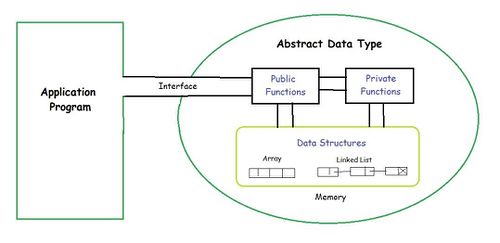
The definition of ADT only mentions what operations are to be performed but not how these operations will be implemented. It does not specify how data will be organized in memory and what algorithms will be used for implementing the operations. It is called “abstract” because it gives an implementation-independent view. The process of providing only the essentials and hiding the details is known as abstraction.
The user of data type does not need to know how that data type is implemented, for example, we have been using Primitive values like int, float, char data types only with the knowledge that these data type can operate and be performed on without any idea of how they are implemented. So a user only needs to know what a data type can do, but not how it will be implemented. Think of ADT as a black box which hides the inner structure and design of the data type.[2]
There are two parts to each ADT:
- The public or external part, which consists of:
- the conceptual picture (the user's view of what the object looks like, how the structure is organized)
- the conceptual operations (what the user can do to the ADT)
- The private or internal part, which consists of:
- the representation (how the structure is actually stored)
- the implementation of the operations (the actual code)
In general, there are many possible operations that could be defined for each ADT; however, they often fall into these categories:
- initialize
- add data
- access data
- remove data
Examples of Abstract Data Type (ADT)[3]
Some examples of ADT are Stack, Queue, List etc. Below are some operations of these mentioned ADT −
- Stack −
- isFull(), This is used to check whether stack is full or not
- isEmpry(), This is used to check whether stack is empty or not
- push(x), This is used to push x into the stack
- pop(), This is used to delete one element from top of the stack
- peek(), This is used to get the top most element of the stack
- size(), this function is used to get number of elements present into the stack
- Queue −
- isFull(), This is used to check whether queue is full or not
- isEmpry(), This is used to check whether queue is empty or not
- insert(x), This is used to add x into the queue at the rear end
- delete(), This is used to delete one element from the front end of the queue
- size(), this function is used to get number of elements present into the queue
- List −
- size(), this function is used to get number of elements present into the list
- insert(x), this function is used to insert one element into the list
- remove(x), this function is used to remove given element from the list
- get(i), this function is used to get element at position i
- replace(x, y), this function is used to replace x with y value
Benefits of Using Abstract Data Types[4]
Code is easier to understand (e.g., it is easier to see "high-level" steps being performed, not obscured by low-level code).
Implementations of ADTs can be changed (e.g., for efficiency) without requiring changes to the program that uses the ADTs.
ADTs can be reused in future programs.
Fortunately for us, object-oriented programming languages (like Java) make it easy for programmers to use ADTs: each ADT corresponds to a class (or Java interface - more on this later) and the operations on the ADT are the class/interface's public methods. The user, or client, of the ADT only needs to know about the method interfaces (the names of the methods, the types of the parameters, what the methods do, and what, if any, values they return), not the actual implementation (how the methods are implemented, the private data members, private methods, etc.).
See Also
References
- ↑ What is Abstract Data Type (ADT)? Wikipedia
- ↑ Understanding Abstract Data Types GeeksforGeeks
- ↑ Examples of Abstract Data Type (ADT) Tutorials Point
- ↑ Benefits of Using Abstract Data Types University of Wisconsin