Albers Equal Area Conic Projection

The Albers equal-area conic projection, is a map projection that uses two standard parallels to reduce some of the distortion of a projection with one standard parallel. Although neither shape nor linear scale is truly correct, the distortion of these properties is minimized in the region between the standard parallels. This projection is best suited for land masses extending in an east-to-west orientation rather than those lying north to south. It is used by the USGS for maps showing the conterminous United States (48 states) or large areas of the United States, as well as for many thematic maps.

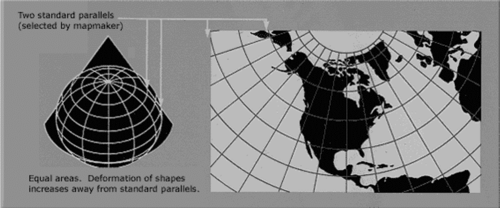
source: USGS

First developed by Heinrich Christian Albers in the early nineteenth century for European maps, its biggest success has been for maps of North America—specifically, for maps for the conterminous United States.

The Albers projection is one of the standard projections for British Columbia, and is the sole standard projection used by the government of Yukon. It is also used by the United States Geological Survey and the United States Census Bureau. Snyder (Section 14) describes generating formulae for the projection, as well as the projection's characteristics. Coordinates from a spherical datum can be transformed into Albers equal-area conic projection coordinates with the following formulas, where λ is the longitude, λ0 the reference longitude, φ the latitude, φ0 the reference latitude and φ1 and φ2 the standard parallels.

The Albers Area Projection Fomulae
Let phi_0 be the latitude for the origin of the Cartesian coordinates and lambda_0 its longitude, and let phi_1 and phi_2 be the standard parallels. Then for a unit sphere, the Albers equal-area conic projection maps latitude and longitude (phi,lambda) to Cartesian (x,y) coordinates

x = rhosintheta y = rho_0-rhocostheta,

where

n = 1/2(sinphi_1+sinphi_2) theta = n(lambda-lambda_0) C = cos^2phi_1+2nsinphi_1 rho = (sqrt(C-2nsinphi))/n rho_0 = (sqrt(C-2nsinphi_0))/n.

The projection illustrated above takes (phi_0,lambda_0)=(0 degrees,0 degrees) and standard parallels at phi_1=0 degrees and phi_2=60 degrees.

The inverse formulas are

phi = sin^(-1)((C-rho^2n^2)/(2n)) lambda = lambda_0+theta/n,

where

rho = sqrt(x^2+(rho_0-y)^2) theta = tan^(-1)(x/(rho_0-y)).

See Also

In cartography and geographic analyses, the Albers Equal Area Conic Projection is a pivotal tool for representing spatial relationships on maps, ensuring area accuracy across vast regions. This map projection is favored for thematic and regional maps where area fidelity is paramount, such as agricultural planning, environmental studies, and resource management. To enrich the understanding of the Albers Equal Area Conic Projection within the broader context of geography, cartography, and spatial analysis, delving into the following related topics is highly beneficial:

• Map Projections and Cartography: An overview of the science and art of map making, including the theoretical basis behind different types of map projections and their specific uses in conveying spatial information accurately.
• Spatial Data Analysis: Techniques and tools used to analyze spatial data to identify patterns, relationships, and trends across geographic areas, emphasizing the implications of projection choices on spatial analysis outcomes.
• Geographic Coordinate Systems: Exploration of coordinate systems used to define positions on the Earth's surface, highlighting the transformation processes between geographic (lat/long) and projected coordinate systems.
• Thematic Mapping: This topic discusses the creation and interpretation of maps designed to highlight specific themes or subjects, such as population density, climate variations, or land use, where equal-area projections may be particularly relevant.
• GIS and Spatial Modeling: The use of Geographic Information Systems (GIS) for modeling spatial relationships and processes, including the role of different projections in spatial data representation and analysis.
• Environmental Planning and Management: Exploration of how spatial data and projections inform environmental conservation efforts, resource management, and policy development, ensuring accurate area assessments for sustainable decision-making.
• Agricultural Land Use Planning: This section discusses the application of spatial data and equal-area projections to optimize agricultural land use, including crop planning, irrigation management, and yield estimation.
• Climate Change Analysis: Using spatial data and appropriate projections to model and analyze the impacts of climate change on various geographic regions, supporting mitigation and adaptation strategies.
• Remote Sensing and Satellite Imagery: Techniques for acquiring and analyzing imagery and other data collected by satellites or aerial sensors, including considerations for map projections in data processing and analysis.
• Digital Elevation Models (DEM): This section discusses the creation and use of DEMs to represent the Earth's surface elevation, including how projections influence the interpretation of topographic data.
• Data Visualization and Cartographic Design: This course outlines the principles of designing clear, informative, and visually appealing maps, emphasizing the importance of choosing appropriate projections for the map's purpose and audience.
• Geospatial Data Standards and Quality: Covers the standards for geospatial data collection, sharing, and quality control, including the role of map projections in ensuring data interoperability and accuracy.
• Ethical Considerations in Cartography and GIS: Discuss ethical issues in geographic data representation and analysis, including concerns over projection choices that can influence perceptions of area and space.

Exploring these topics provides a comprehensive backdrop to the Albers Equal Area Conic Projection, underscoring its significance, inaccurate area representation, and its applications across a multitude of disciplines. This exploration highlights the strategic role of map projections in supporting informed decision-making, spatial analysis, and the visual communication of geographic information.

References

Further Reading

• Albers Equal Area Conic ArcGIS Desktop
• Europe Albers Equal Area Conic Spatial Reference