Cluster Analysis
What is cluster analysis?
Cluster analysis is a process of grouping data points together so that they can be analyzed as a unit. This process is used in various fields, including marketing, sociology, and psychology. There are many different techniques for cluster analysis, and the choice of technique depends on the nature of the data and the goals of the researcher. The most common way to evaluate the quality of a cluster is by its purity: how homogeneous it is within itself and how heterogeneous it is with other clusters. There are also many different ways to measure the distribution of clusters, including methods based on distance, density, and connectivity. Applications of cluster analysis include segmentation (identifying groups within a population), classification (assigning data points to pre-defined groups), and outlier detection (finding unusual data points).
The significance of cluster analysis is that it provides a powerful tool for making sense of complex data sets. By grouping together similar objects into categories, it helps to uncover structures and patterns in the data that would otherwise be difficult or impossible to detect. Cluster analysis can be used to identify trends and associations between different groups of items, as well as to identify groups of people with similar buying habits. Moreover, distance is an important measure used in cluster analysis which can help reveal the relationships between different sets of data points.
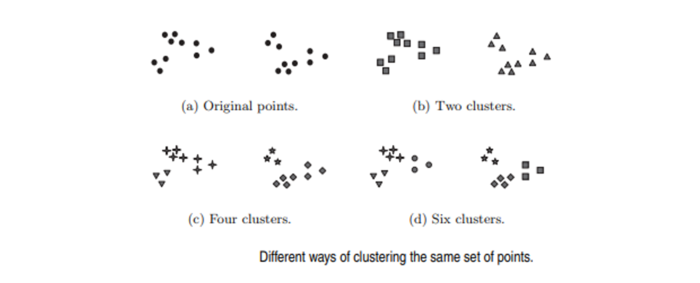
In many applications, the notion of a cluster is not well defined. To better understand the difficulty of deciding what constitutes a cluster, consider The Figure below, which shows twenty points and three different ways of dividing them into clusters. The shapes of the markers indicate cluster membership. Figures (b) and (d) divide the data into two and six parts, respectively. However, the apparent division of each of the two larger clusters into three subclusters may simply be an artifact of the human visual system. Also, it may not be unreasonable to say that the points form four clusters, as shown in Figure (c). This figure illustrates that the definition of a cluster is imprecise and that the best definition depends on the nature of the data and the desired results.
Cluster analysis is related to other techniques that are used to divide data objects into groups. For instance, clustering can be regarded as a form of classification in that it creates a labeling of objects with class (cluster) labels. However, it derives these labels only from the data.
What are the techniques used in cluster analysis?
- Hierarchical cluster analysis: Hierarchical cluster analysis is a technique used in cluster analysis for grouping data into clusters based on the similarity of their values. The process begins by placing each subject in its own cluster and then gradually merging the clusters until all subjects are in one single group. Hierarchical clustering is often used to group data into different categories or tiers, and it can be useful for identifying patterns or trends within a dataset.
- K-means clustering: K-means clustering is an iterative algorithm that is frequently used in clustering analysis. It can be employed for exploratory data analysis, anomaly detection, and segmentation. When the data is non-convex, more sophisticated techniques are needed. Unsupervised methods such as dimensionality reduction and feature ranking can be used to determine groupings in the data. K-means clustering on the other hand is a supervised method that helps discover groupings in the data.
- Model-based clustering: Model-based clustering is a data-driven approach to cluster analysis that uses statistical models to identify clusters of data. This method works by trying to find a model which best fits the data and then assigning the objects into clusters accordingly. It can be used to group objects together according to their attributes and capture correlations or dependencies between them. Model-based clustering can also be used for identifying outliers from the data set, as well as for Gaussian mixture model clustering, which involves grouping items into clusters using a Gaussian distribution. Finally, other density-based clustering methods such as Expectation Maximization (EM) are sometimes necessary when dealing with denser datasets that cannot be modeled using Gaussians.
- Fuzzy clustering: Fuzzy clustering is a technique used to group objects together that are similar but not exactly the same. It differs from other clustering techniques in that it allows for greater flexibility in grouping data by using a distance function to measure the similarity between objects and clusters. This allows for different merging strategies depending on the desired clustering pattern. Additionally, fuzzy clustering allows for more flexibility than other methods as it can incorporate information about clusters such as whether observations are known to belong to them or not.
- Density-based clustering: Density-based clustering is a type of data mining technique used in cluster analysis to identify clusters of points that are close together and to differentiate them from points that are far away. It looks for clusters in data sets by exploring the points around it, using a radius to determine if two objects are within close proximity. DBSCAN (Density-Based Spatial Clustering of Applications with Noise) is one popular density-based clustering algorithm that uses this density-reachability model; it is fast and easy to use, requiring only a linear number of range queries on the database. Other algorithms such as EM clustering, Mean Shift, and OPTICS are also often used in cluster analysis for different applications or objectives.
- Grid-based clustering: Grid-based clustering is a technique used in cluster analysis to compare data sets by creating clusters from adjacent groups of dense grids. It works by dividing the data into smaller units, known as grids, and comparing the density of each grid to a predetermined threshold. If the density of a grid is lower than the threshold, that grid is eliminated. Several different algorithms can be employed in clustering analysis, including STING and CLIQUE. Grid-based clustering allows for grouping data according to similarity and provides an efficient way to analyze multi-dimensional data sets.
- Subspace clustering: Subspace clustering is a machine learning algorithm used to cluster data that has been partitioned into a number of subspaces. It allows clusters to be identified based on similarities between the data items in different subspaces. This technique can be used in cluster analysis, where it is employed to identify relationships and patterns within the clustered data. For example, CLIQUE and SUBCLU are two algorithms that use subspace clustering for this purpose. Mutual information can also be employed as a measure of how similar two items are, with belief propagation leading to the development of new clustering algorithms that make use of this metric. Additionally, genetic algorithms have been used to optimize different fit functions related to mutual information for further insight into any given dataset.
- Constraint-based clustering: Constraint-based clustering is an approach to dividing data into clusters that meet two conditions: each partition should belong to only one cluster and there should be no empty clusters. This technique is suitable when there are limited resources available and the data needs to be clustered in a way that is easily understood. Instead of using traditional partitioning algorithms, constraint-based clustering uses frequency statistics of how often an object appears in a cluster to determine the number of clusters automatically. Additionally, this method can also reflect the spatial distribution of data points.
- Spectral clustering: Spectral clustering is a type of cluster analysis algorithm that transforms the input data into a graph-based representation, which can help to better separate clusters than in the original feature space. This technique is based on computing the eigenvectors of a similarity matrix associated with the data set, and then grouping points based on these eigenvectors. Spectral clustering can be used in many applications such as image segmentation, text categorization, dimensionality reduction, and more.
- Distribution-based clustering: Distribution-based clustering is a type of clustering that takes into consideration the correlation and dependence between attributes in a data set. It is used to identify clusters in datasets with non-Gaussian distributions, by using more complex algorithms than those used for datasets with Gaussian distributions. This method allows for a more effective and accurate representation of the clusters present in the data set.
What is the process of performing a cluster analysis?
Step 1: Build and distribute a survey: It is important to build and distribute a survey before conducting a cluster analysis in order to reduce data complexity and gain insight into customer propensity to purchase and preferences for the product. By building a survey with multiple measures, it is possible to identify similar characteristics within the data that can then be grouped together into clusters. This allows for more accurate predictions of customer behavior as well as more accurate results from the cluster analysis. It is essential to build and distribute a survey when calculating purity and distribution in cluster analysis in order to gain a better understanding of customer behavior. By collecting data through surveys, companies can measure the propensity of customers to purchase products or services as well as their preferences. This data can then be used for performing factor analysis, which reduces the number of factors being analyzed. Finally, cluster analysis can be used for determining how many clusters are appropriate and assign them accordingly. Through this process, companies will be able to assess both the purity and distribution of customer clusters regarding their purchasing behavior and preferences.
Step 2: Analyze response data: When performing a cluster analysis, it is important to analyze response data in order to accurately identify similarities and differences between the cases being clustered. This can be done by using a suitable measure of similarity, such as Z-scores, or standardizing the data across cases. By analyzing response data during a cluster analysis, patterns and trends in the data can be more easily identified. To calculate purity and distribution in cluster analysis, one must first create a data table that represents each subject's data. Then, they need to select the Analyze->Classify->Hierarchical Cluster menu path to obtain the dialogue box for calculating purity and distribution. They can then specify the number of clusters to be generated by SPSS or choose a range of clusters. Additionally, they must select between between-groups linkage (average linkage) or one of several other methods as well as which type of data should be analyzed (interval, frequency or binary). It is also important that they standardize across cases by converting their data into Z-scores before proceeding with the calculation by clicking on the "Calculate" button.
Step 3: Take informed action: The final step in performing a cluster analysis is to produce a report, which will include information about the clusters found, including the number of nodes and types of nodes in each cluster. Additionally, it is also necessary to identify forks in the data which represent high similarity and create a dendrogram that divides cases into two groups based on their score on intrusive thoughts and impulsive thoughts and actions. It is important to take informed action when calculating purity and distribution in cluster analysis because the accuracy of the results depends on the quality of the data used. If a proper assessment isn't made, there is a chance that inaccurate results will be produced. Taking informed action helps ensure that any conclusions drawn from cluster analysis are reliable and meaningful.
Step 4: Perform hierarchical cluster analysis: Hierarchical cluster analysis is important in the process of performing a cluster analysis because it allows analysts to group data into meaningful clusters. This information can be used to improve the accuracy of cluster analyses and make more informed decisions about data analysis. Hierarchical clustering also provides a visual representation of how cases are being clustered together based on their similarities. This helps analysts better interpret and understand the results of their cluster analysis, which can ultimately lead to more meaningful insights from the data. To perform hierarchical cluster analysis, one must first standardize the data, select the method of clustering (between-groups or average linkage), choose the options, and create a variable to store the cases in clusters. Then, they can use SPSS to specify the number of clusters to be created and inspect the output of the cluster analysis for substantive sub-clusters. Other useful techniques include measuring the similarity between data sets using different methods offered by SPSS and standardizing variables in order to analyze data accurately using Q-analysis. Finally, one can save a new variable that contains coding values for cluster membership and view results with an icicle plot or more interpretable dendrogram.
Step 5: Identify clusters: When performing a cluster analysis, one must first identify clusters by assessing the similarity of different objects. If two objects are similar, they are added to a cluster. If an object is relatively similar to two other objects in a cluster, it is added to the cluster. The process of determining clusters is hierarchical and based on similarity and can be visualized as a dendrogram or tree diagram. Clusters are identified by calculating the average similarity between all remaining cases and adding cases that have an average above the cutoff value to them.
Step 6: Interpret results of cluster analysis: Interpreting the results of a cluster analysis requires creating a variable to store the cluster information. SPSS does not create this variable by default, so this must be done manually. Once that is done, the results of the cluster analysis can be interpreted and used to group similar data sets together. The results show that there is a high degree of similarity between groups and provide insight into how clusters are distributed and organized. Additionally, by examining the icicle plot or dendrogram one can also gain an understanding of how pure each cluster is in terms of its members containing varied data points within it.
Step 7: Refine clusters: It is important to refine clusters in cluster analysis in order to ensure accuracy and optimize the results. By using an iterative approach, the algorithm can determine which cases should be added or removed from each cluster, allowing for faster and more accurate clustering. Additionally, a distance matrix can be used to measure the distance between data points and help determine how many clusters should be retained. Refining clusters helps produce more meaningful results that are tailored to the data being examined.
Step 8: Take action based on findings: The findings of a cluster analysis should be used to improve the design of the system. This can involve understanding how the data was analyzed, which can be done by looking at the dendrogram output from SPSS. The cases within each cluster should then be analyzed based on their relative positions in order to gain insights about patterns and features that are shared between them. Through this process, new approaches for system design and development can be developed in order to better meet user needs and optimize performance.
How to calculate purity and distribution in cluster analysis?
- Calculate cluster purity: Calculating the purity and distribution of data points in a cluster is an important part of cluster analysis. It helps to determine how homogenous or heterogeneous a given set of data points is, and can help guide decisions about which clusters to retain after a hierarchical clustering algorithm has been used. Purity and distribution measures can also be used to evaluate the effectiveness of different clustering algorithms when they are applied to similar datasets.
- Calculate cluster distribution: Calculating purity and distribution in cluster analysis requires repeating steps 3-5 multiple times. In step 3, the K-means clustering algorithm is used to partition data points into a number of clusters with the optimal value for K being configured by the user. Step 4 involves calculating distances between points and the cluster means using Euclidean distance. Step 5 finds new cluster means by taking every data point in a particular cluster and calculating a mean, which is then used to determine which points should be added to the clusters in *Interpret the results: Interpreting the results of a cluster analysis requires creating a variable that tells SPSS how to group cases. The default method of grouping cases in SPSS may not be suitable for cluster analysis, so one should consider using other methods such as Euclidean or another measure of similarity. Additionally, it is important to standardize the variables when clustering cases and across cases when clustering variables. Once this is done, an icicle plot or dendrogram can be used to visualize the results and help with interpretation. By looking at these visualizations, patterns in data can be identified which can give insight into how it is organized and behaves.
What are some applications of clustering algorithms?
- Segmentation of customers based on buying habits: Clustering algorithms can be used to segment customers into different groups based on their buying patterns and interests. This allows companies to better position themselves, explore new markets, and develop products that specific clusters find relevant and valuable. Additionally, cluster analysis can be used by finance and real estate professionals to assess the real estate potential of different parts of a city as well as by marketing professionals to develop market segments that allow for better positioning of products and messaging.
- Targeted marketing campaigns: Clustering algorithms can help with targeted marketing campaigns by allowing marketers to group customers into distinct categories and identify them more easily. These clusters can then be used to better understand customer characteristics, behaviors, and preferences, as well as target specific segments of the market with tailored messaging. By using clustering algorithms in their marketing strategies, businesses are able to increase the effectiveness of their campaigns while reaching more potential customers.
- Detecting fraudulent activities: Clustering algorithms are effective in detecting fraudulent activities because they can identify discrete groups of objects, customers, or other types of data that have similarities. By grouping related data together, it is easier to recognize patterns and anomalies that may indicate fraudulent activity. This can help organizations quickly detect suspicious transactions and stop fraud before losses occur. Additionally, cluster analysis can be used for a variety of applications such as medical imaging to segment radiation treatments and classify antimicrobial compounds which further helps organizations be better equipped to handle fraudulent activities.
- Text mining and document clustering: Clustering algorithms have many applications in text mining and document clustering. For example, they can be used to group traffic sources more accurately and target marketing messages more effectively; help sales teams identify prospects; manage high volumes of documents more effectively; identify patterns and themes in a dataset; and organize large data sets. Text mining and document clustering can be used for a variety of purposes such as social network analysis or medical image tissue clustering. Clustering algorithms are useful for helping organizations gain insight from their data by grouping it into meaningful clusters that can reveal important trends in the data set.
- Network analysis and social media clustering: Clustering algorithms can be used for network analysis and social media clustering to identify patterns and structures within large groups of people. These algorithms can group individuals based on similarities of characteristics, such as similar interests or opinions. This type of analysis can be used to understand the relationships between different nodes in a social network and identify communities within them. Additionally, cluster analysis can also help uncover hidden relationships between different users in a social media platform, providing insights into how user behavior is organized and interconnected.
- Image analysis and object recognition: Clustering algorithms help image analysis and object recognition by providing grouping of similar images or objects together, finding the best-scoring set of parameters for recognizing objects, identifying patterns and labels in unfamiliar data, and analyzing spatial point patterns. Popular clustering algorithms used for this purpose include K Function, radial distribution functions, DBSCAN, convolutional neural networks (CNNs), and machine learning techniques such as neural networks. Localization microscopy data is not immediately compatible with CNNs but can be adapted to work with these clustering algorithms to improve image analysis and object recognition.
- Recommendation systems: Clustering algorithms can help recommend items to users by grouping similar objects together. By doing so, they are able to identify patterns in user preferences and suggest items that fit their tastes. Different clustering algorithms can be used for different purposes, such as classification, regression, and dimension reduction. Additionally, clustering is often used in combination with other machine learning techniques such as classification and regression in order to improve recommendations for users.
- Anomaly detection: Clustering algorithms can be used for anomaly detection by analyzing data points that lie outside predetermined clusters. By grouping data points into clusters, and then using a metric such as distance or density to measure each cluster's characteristics, anomalies can be identified and isolated from the rest of the dataset. This allows for more accurate identification of outliers that would otherwise have gone unnoticed. Additionally, clustering algorithms can help identify suspicious patterns in large datasets which could indicate fraudulent activity.
- Medical diagnosis and disease clustering: Clustering algorithms can be used in medical diagnosis to help doctors identify patterns among different symptoms, diagnoses, and demographic information. These algorithms can also be used to group similar objects according to characteristics such as location or weighting, helping doctors find the most relevant information quickly. Additionally, clustering algorithms can improve accuracy in medical diagnosis by optimizing criteria such as analysis of multicenter research.
- Market segmentation and risk management: Clustering algorithms can be used to identify and target specific groups of customers for market segmentation, allowing companies to better position themselves in the market and explore new markets. Additionally, clustering algorithms can be used for risk management by helping companies assess customer risk levels and develop cost-effective strategies to manage risk. These algorithms can also help companies develop products that are tailored to the needs of specific clusters, thus increasing sales and profitability.
What are cluster data points?
A data point is an individual record in a dataset. Data points can be clustered by grouping them together based on similarities between their attributes and characteristics. This process of clustering can be done using grid-based techniques, which divide the data into cells and randomly select one to start the process. The technique then identifies dense clusters of data points within each cell, using a threshold value, that are marked as clusters before continuing to identify any further cells that may contain clusters of data points. Clustering is used to find the best model fit for the given dataset by taking outlier or noise into account in order to generate robust clustering methods.
What is the k-means clustering algorithm?
The k-means clustering algorithm is an iterative partition algorithm that works by randomly assigning data points to clusters. The aim of the algorithm is to find a partition that best suits the data. The distance between two points is used to decide which data point should be added to a cluster and it can be modified to determine the optimal number of clusters. Through this process, the algorithm divides data into clusters and assigns a new mean for each cluster. As such, it groups similar data points together into new clusters based on their similarities, allowing for more efficient analysis of datasets. By recalculating new cluster means after data points have been added or removed, this method offers great accuracy in its analysis and produces reliable results with minimal computational effort.
What are the different types of linkage clustering?
Linkage clustering is an unsupervised learning technique used to find clusters in datasets. There are three different linkage clustering methods: Simple, Ward's, and Average Linkage. Simple Linkage measures the average similarity between cases and then merges them together to reduce variability. Ward's Method attempts to minimize the variance within a cluster by joining cases together using the sum of squared deviations to measure how well a case fits into a cluster. The Far Neighbour Method is used if two cases with the highest similarity are not suitable as the nucleus of the cluster while Complete Linkage is used when two cases with the highest similarity are unsuitable as the nucleus of that cluster. Overall, linkage clustering relies on the overall similarity between data points rather than any single point’s similarities for successful clustering results.
How do you evaluate the results of a clustering algorithm?
Evaluating the results of a clustering algorithm requires a variety of methods. Internal measures such as the Silhouette coefficient are used to determine how well clusters match samples, and subjective evaluations based on similarity within and between clusters is also employed. The best score is given to algorithms that produce clusters with high similarity within and low similarity between clusters. Additionally, it must be established that the data set has a structure that the algorithm is designed to recognize for validity purposes. As such, various measures can be used for assessing quality, such as the Davies–Bouldin index, which takes into account the distribution of elements within each cluster when determining performance metrics.
What are the different types of cluster models?
Cluster models are used to group objects together based on their similarities or other characteristics. There are various different types of cluster models, each with its own properties and uses. Connectivity models link data points based on their proximity in the dataset, centroid models use the center point of a cluster as a reference point for grouping data points, and distribution models use multivariate normal distributions to model clusters. Group model clustering does not provide an exact model while graph-based clustering uses graphs to group data points together. Hard clustering assigns objects to a single set while soft clustering allows them to exist in multiple sets at once. Cluster analysis is used for classification by developing decision rules that define which sets each object is assigned to and using it for application-oriented purposes such as workload type or density calculation modeling.
What are the different types of similarity measures?
The different types of similarity measures are important because they provide a way to measure how similar two cases are. These measures help researchers group cases based on their similarities, allowing them to identify patterns and relationships between the data. The most commonly used similarity measures include similarity coefficients, dissimilarity coefficients, hierarchical clustering methods, and other criteria-based methods. Similarity coefficients measure the degree of similarity between two or more cases, while dissimilarity coefficients measure the degree of difference between those same cases. Hierarchical clustering methods then merge clusters of similar cases together based on their similarities or differences measured by these criteria. All these different techniques play an important role in cluster analysis by helping researchers identify related groups within data sets.
What are the different types of evaluation criteria?
Different types of evaluation criteria can have a significant impact on the final decision. Some evaluation measures are based on intuition rather than data, which can lead to biased results. Other evaluation criteria are used to assess the quality of clustering algorithms, such as the Davies–Bouldin index and other measures that look at distances between elements in a cluster and the number of clusters. These different types of evaluation criteria need to be carefully assessed when making decisions so that an accurate prediction is made regarding cluster quality.
See Also
Analysis Process Model (APM)
Analysis Effort Method