Process Capability

Process Capability(C_p) is a measurable property of a process to the specification expressed as a process capability index (e.g., C_pk or C_pm) or as a process performance index (e.g., P_pk or P_pm). The output of this measurement is often illustrated by a histogram and calculations that predict how many parts will be produced out of specification (OOS). Two parts of process capability are 1) measure the variability of the output of a process, and 2) compare that variability with a proposed specification or product tolerance.

Process Capability Index (C_pk)
Process capability index (C_pk) is a statistical tool, to measure the ability of a process to produce output within a customer’s specification limits. In simple words, it measures the producer’s capability to produce a product within the customer’s tolerance range. C_pk is used to estimate how close you are to a given target and how consistent you are around your average performance. C_pk gives you the best-case scenario for the existing process. It can also estimate future process performance, assuming performance is consistent over time. C_pk is a standard index to state the capability of one process, the higher the C_pk value the better the process is. For instance, Machine 1 has a C_pk of 1.7 and machine 2 has a C_pk of 1.1. From the C_pk value, one can derive that Machine 1 is better than 2. Since C_pk uses specification limits and parts variation (sigma), we can also arrive at the yield processed and losses from the machine.

Cpk is a standard index to state the capability of one process, the higher the Cpk value the better the process is. For instance, Machine 1 has a Cpk of 1.7 and machine 2 has a Cpk of 1.1. From the Cpk value, one can derive that Machine 1 is better than 2. Since Cpk uses specification limits and parts variation (sigma), we can also arrive at the yield processed and losses from the machine.

Cpk	Process Yield
0.5	86.8%
0.8	98.4%
1.0	99.7%
1.2	99.97%
1.33	99.99%

C_pk = or >1.33 indicates that the process is capable and meets specification limits. Any value less than this may mean variation is too wide compared to the specification or the process average is away from the target.

Measuring Process Capability
The capability indices can be calculated manually, although there are several software packages available that can complete the calculations and provide graphical data illustrating process capability. For the example in this section, we will utilize a popular statistical software package. For our example, we will utilize data from randomly collected measurements of a key characteristic of a machined part. To better represent the population values, the sample data must be randomly collected, preferably over time from a large production run. A few things to keep in mind:

• Our data is quantitative and variable
• Our data consists of 100 measurements
• The target dimension is 25.4 mm
• USL (Upper Specification Limit) = 25.527 mm
• LSL (Lower Specification Limit) = 25.273 mm
• Range = 0.254 mm

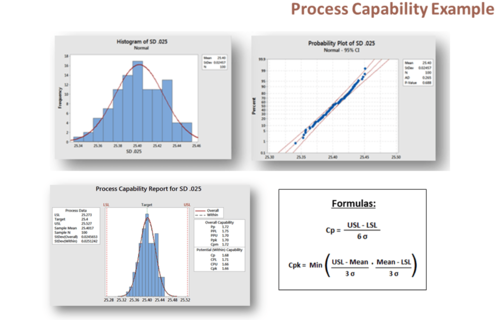
First, we will examine our data with a simple histogram to determine if it could fit a normal distribution. In addition, we can generate a probability plot evaluating our data’s best fit to a line further indicating we are 95% confident that our data fits a normal distribution.

source: Quality One

Now let us examine the Process capability report:

• C_p (Process Capability) = 1.68
• C_pk (Process Capability Index) = 1.66

Using the graph, we can further evaluate process capability by comparing the spread or range of the product specifications to the spread of the process data, as measured by Six Sigma (process standard deviation units).

Through examination of the reports, we can determine that our example process is in a state of statistical control. All the data points fall well within the specification limits with a normal distribution. A process where almost all the measurements fall inside the specification limits is deemed a capable process. Process capability studies are valuable tools when used properly. As previously mentioned the information gained is generally used to reduce waste and improve product quality. In addition, by knowing your process capabilities, the design team can work with manufacturing to improve product quality, and processes that are “not in control” may be targeted for improvement. During a typical Kaizen event or other quality improvement initiatives, Process Capability is calculated at the start and end of the study to measure the level of improvement achieved. Accurate knowledge of process capability enables management to make decisions regarding where to apply available resources based on data.

See Also

Process Capability is a statistical measure of a process's ability to produce output within specified limits. It relates to the inherent variability of a process under statistical control and compares that variability to the allowed tolerance or specifications. This measure is vital in manufacturing, quality control, and Six Sigma projects to determine how well a process can meet customer requirements. Understanding process capability helps organizations optimize their processes, reduce waste, and improve product quality and consistency.

• Statistical Process Control (SPC): Discussing the quality control method that employs statistical methods to monitor and control a process. SPC helps in identifying whether a process is stable and capable.
• Six Sigma: Covering the set of techniques and tools for process improvement, focusing on reducing process variation and improving quality. Process capability is a key concept in Six Sigma for measuring the performance of a process.
• Quality Control (QC): Explaining the practices and procedures used to ensure that a product or service meets specified requirements. QC often involves assessing process capability to ensure processes are performing adequately.
• Capability Index (Cpk and Cp): Discussing specific measures of process capability, including Cpk, which measures how close a process is performing to its specification limits, and Cp, which measures the potential capability of a process if it were centered.
• Lean Manufacturing: Covering the systematic method for waste minimization within a manufacturing system without sacrificing productivity. Understanding process capability is important in Lean to ensure that process improvements lead to products that meet customer specifications.
• Total Quality Management (TQM): Discussing the management approach to long-term success through customer satisfaction, where process capability analysis plays a role in understanding and improving process quality.
• Design of Experiments (DOE): Explaining the methodology for systematically applying statistics to the experimental process. DOE can be used to improve process capability by identifying key process variables affecting output quality.
• Control Charts: Covering the tools used in SPC for tracking process performance over time. Control charts help in identifying variations that may affect process capability.
• Value Stream Mapping: Discussing the lean-management method for analyzing the current state and designing a future state for the series of events that take a product or service from its beginning through to the customer, with an eye towards improving process capability.
• ISO 9001: Explaining the international standard for a quality management system (QMS). The standard provides guidelines and requirements for organizations to ensure that their products and services consistently meet customer requirements, including maintaining capable processes.
• Pareto Principle Analysis: Discussing the technique for decision-making used in quality control and project management. It's based on the Pareto Principle, which helps prioritize the causes of process variability affecting process capability.
• Benchmarking: Covering the practice of comparing business processes and performance metrics to industry bests and best practices. Benchmarking can help organizations understand how their process capabilities stack up against those of leaders in their sector.