Chaos Theory
What is the Chaos Theory?
The Chaos Theory is an area of deterministic dynamics that has applications in many fields, including IT. It is based on the idea that small changes in initial conditions can lead to large differences in future outcomes, which contradicts the scientific community's expectations. The Chaos Theory helps explain some of the unpredictability experienced when using Newtonian physics and why the accuracy of measurement does not reduce uncertainty in predictions.
Chaos theory in mathematics
Chaos theory is a branch of mathematics that studies the behavior of dynamical systems, which are sensitive to initial conditions. This field has enabled researchers to better understand and predict the behavior of complex systems such as social systems. While chaos is often associated with unpredictability, many chaotic systems have patterns and trajectories that can be predictive in nature. Chaos theory has led to the development of new mathematical models, allowing for a more detailed understanding of how complex physical and social phenomena function. With its potential for uncovering insights into our universe at large, chaos theory has continued to fascinate scientists looking for solutions to problems.
The significance of chaos theory lies not just in its ability to help scientists understand and predict the behavior of complex systems, but also in its potential for revealing insights into the workings of our universe as a whole – something that has excited some researchers even more than its potential for providing solutions to problems!
Examples of chaos theory in mathematics
- Deterministic Nonperiodic Flow: Deterministic nonperiodic flow is a type of behavior characterized by unpredictable changes over time. It is related to chaos theory in that it explains how seemingly simple physical systems can display chaotic behavior. This type of flow involves the iteration of a function or system which produces an irregular, but consistent pattern over time. These patterns are often reflected in the form of fractals, which are objects with the same degree of complexity on all scales. Computer packages are available to calculate some aspects such as these and measure their complexity and unpredictability.
- Nonlinear Models, Faithfulness, and Confirmation: Chaos theory deals with the behavior of systems that are sensitive to initial conditions. It seeks to understand how small variations in initial conditions can affect the long-term behavior of a system, leading it in unexpected directions. Chaos theory has become increasingly important for mathematicians seeking accurate models for physical or economic phenomena, as it allows for successive refinements of models and data in order to better represent the idiosyncrasies and complexity found in nature. This makes chaos theory an invaluable tool for predicting and controlling systems with unpredictable behavior.
- The Nature of Chaos Explanations: Chaos theory focuses on understanding complex systems that are out of equilibrium. It suggests that there are underlying mechanisms or processes behind chaotic behavior and studies how these systems can become unpredictable and seemingly random. Chaos theory is taken as a necessary condition for SD, or exponential divergence of neighboring trajectories, and can be used to confirm models. In addition, chaos theory helps us to understand patterns and structures in mathematics, as well as how chaotic systems can behave in unpredictable ways. This information can be used to improve our understanding of complex mathematical systems.
- Attractors in Geosciences: An attractor in relation to chaos theory is a state where a chaotic system has settled into a stable pattern. In order to achieve an attractor, the system must undergo a change in strategy, such as running parallel inversions instead of cooperating. Attractors are used to understand the behavior of different models and the complex and nonlinear behavior of systems, allowing scientists to reduce complexity and drive processes toward understanding.
- Realism and Chaos: The connection between chaos theory and realism is that chaotic models possess an infinite number of layers of structure, which allows them to remain within a bounded region of state space. This type of structure helps to fold and interconnect trajectories so that they remain within a region. Chaos theory can explain how complex systems can be unpredictable, while realism in mathematics aims to accurately reproduce the behavior of target systems with mathematical models.
- Does Quantum Chaos Exist? Isolated Systems: Quantum chaos is a concept that studies the behavior of complex quantum systems and is important to chaos theory in mathematics. It allows for more accurate predictions when observing chaotic behavior in classical systems and can help uncover universal statistical characteristics of energy spectra, fluctuations, and other phenomena in isolated systems. Additionally, various entropy measures can be used to measure chaos in quantum systems, although there are still questions about which entropy measure is most appropriate for this type of system.
- Does Quantum Chaos Exist? Interacting Systems: Quantum chaos is a subset of chaos theory in mathematics that deals with the behavior of systems that are composed of many interacting components. It is related to classical chaos, which can be detected by measuring Kolmogorov entropy but cannot be accurately measured using Lyapunov exponents. Quantum systems are described by Schrödinger's equation, which is not valid for interacting quantum systems and must instead use Master equations. Chaos theory has revealed universal statistical properties in both isolated and interacting quantum systems, as well as alternative entropy measures to quantify it.
- Free Will and Consciousness: Chaos theory is sometimes used to explore the connection between free will and consciousness. According to chaos theory, small disturbances in the brain can lead to different outcomes in decisions made, and this may account for differences in conscious choices. The amplification process of quantum effects in the brain may be severely constrained, but further research is needed before any definite conclusions can be drawn regarding a connection between free will and consciousness.
- The Validity of the Correspondence Principle: The correspondence principle is important in chaos theory because it suggests that as a quantum system is scaled up, its behavior should become more classical. This helps to explain how classical and quantum systems interact, and it also allows for a relationship between the two systems. Furthermore, the principle ensures that different theories will agree with each other when applied to physical systems. Additionally, if classical chaos does not exist in quantum mechanics then certain predictions based on classical mechanics may not be accurate.
- Conclusions: Chaos theory has implications in mathematics, such as the study of chaos in systems and the development of mathematical models. These can help people understand how chaotic and unpredictable systems can be more efficient than those that are not. Chaos theory also provides a way to acquire knowledge and refine it through steps. Through this, mathematicians can better comprehend how systems work and unlock potentials that were previously unattainable without chaos theory.
The facts about chaos theory in mathematics
- Chaos theory is a field of study which investigates the dynamics of complex systems. It is important because it demonstrates the impact of uncertainty on these systems, and how small errors in initial measurements can lead to large differences in outcomes over time. Edward Lorenz first discovered chaos theory in the early 1960s and since then it has been applied to many different fields, such as IT and weather prediction. By understanding chaos theory, it is possible to better predict how particular systems will respond when exposed to certain changes.
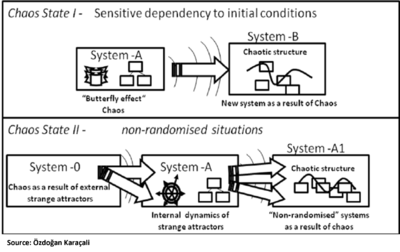
- The eureka moment of chaos theory refers to the publication of a short paper titled "Deterministic Nonperiodic Flow" in 1963 by Edward Lorenz. This paper outlined how small changes can have a large impact on the results. This paper inspired many illustrations and motion pictures, as well as introduced concepts such as the butterfly effect which describe systems that are extremely sensitive to their initial conditions.
- Determinism is an idea that suggests outcomes are determined by the initial conditions of a system. This theory contradicts the basic conventions of physics, as Newtonian physics assumes that measurements can be made with enough accuracy to perfectly predict future outcomes. In practice, however, determinism often leads to wildly different outcomes due to small changes in initial conditions. Chaos theory studies how seemingly random events can lead to complex patterns and behavior stemming from these small changes in initial conditions. By understanding how chaos theory works, scientists can better predict and analyze systems with unpredictable behavior.
- Nonlinearity is an important part of chaos theory that refers to how complex systems change over time. It is used to model the behavior of physical systems, such as the weather, turbulence in liquids, and other patterns. Nonlinearity helps researchers understand how seemingly simple systems can behave unpredictably and it can be measured with computer programs. Chaos theory attempts to explain how nonlinear systems behave in terms of their underlying structure and dynamics, paving the way for a better understanding of chaotic behavior.
- The significance of sensitive dependence on initial conditions in chaos theory is that it demonstrates how small changes in variables can lead to large and unpredictable consequences. This phenomenon was first identified by James Clerk Maxwell, who observed that it occurs in systems with a large number of variables, and later by Henri Poincaré, who found that the same behavior could be seen in systems with a small number of variables. Pierre Duhem also articulated the practical implications of this phenomenon for scientists seeking to deduce mathematical consequences from models. Furthermore, when applied to systems that exhibit symmetry, sensitive dependence on initial conditions can cause instability and unpredictable behavior.
- Chaos theory has a number of implications for the way we think about systems and their ability to respond to change. For example, chaos theory suggests that small changes can have large impacts on systems, making them unpredictable and difficult to manage. It also suggests that deterministic models may not be enough to predict the future health of an economic system. Chaos theory can help organizations understand how random events can have a big impact on their businesses, and it can be used in models in order to improve accuracy.
- Chaos theory has implications for quantum mechanics, with some suggesting that physical quantities can never be predictively accurate. Joseph Ford argued that quantum and Newtonian mechanics should be considered to be equivalent to the point of being "valid physical theories." Ford's description of chaos in relation to the correspondence principle is oversimplified, and it is too simplistic to say that chaos theory fully explains classical phenomena. Chaos theory may help explain some aspects of quantum mechanics but it is not a full explanation. If classical chaos does not exist in quantum mechanics, this could lead to more accurate predictions.
- Chaos theory has significant implications for the Pentagon's office culture. It suggests that small changes in initial conditions can have a large impact on future outcomes, undermining the assumptions of Newtonian physics which rely on precise measurements being possible. Chaos theory also implies that even if measurements are extremely precise, there is still a high level of uncertainty when it comes to predicting future events. This has an impact on how organizations plan for and think about their culture, as it shows that even very small errors in initial conditions can lead to unpredictable results.
How can chaos theory be applied to everyday problems?
- Understanding Nonlinearity and Sensitive Dependence: An understanding of chaos theory can help individuals to solve everyday problems by providing them with insight into complex systems. Chaos theory helps us to better understand how small effects can have dramatic impacts on a system's behavior and how trajectories can diverge or grow away from one another. This knowledge provides insight that allows us to identify nearby trajectories and make use of linear, exponential, and geometric growth rates when attempting to solve everyday problems.
- Assessing the Stability Assumption: The stability assumption is a principle that underlies chaos theory and can be used to assess its accuracy. It states that as uncertainty in the data is reduced, the model behaves in a similar way to the target system. This means that small changes lead to proportional changes in output, and if the linear model is faithful then making small improvements “in the right direction” will lead to improved model performance. Thus it can be used to confirm or disconfirm models based on their accuracy and faithfulness when compared to target systems.
- Exploring the Nature of Chaos Explanations: Chaos theory is a mathematical model used to understand complex systems and their behavior. It relies on the faithful model assumption, which states that our models are accurate representations of the real world. This theory suggests that there might be mechanisms or processes behind chaotic behavior, and it can be used to solve everyday problems such as predicting the behavior of systems, determining when to switch a product from inventory, or understanding how different phenomena (e.g. stretching and folding) can be linked together. By understanding how unpredictable systems can behave in ways that defy expectations, chaos theory can help us to better comprehend actual-world systems and solve everyday problems.
- Examining the Validity of the Correspondence Principle: Chaos theory can be used to understand and predict complex systems. This is done by examining the correspondence principle between quantum and classical mechanics, which states that any two valid physical theories which share a domain of validity must share predictions for physical observations. Additionally, chaos theory can help us understand how systems are interconnected and how they change over time. As Ford's description of chaos bespeaks a misunderstanding of the relationship between the classical and quantum worlds, it is important to note that chaos theory does not apply directly to quantum mechanics, but may explain the chaos in classical systems.
- Examining the Implications of Quantum Chaos: The implications of quantum chaos are far-reaching and have been a major area of research for many years. Researchers have studied the statistical properties of quantized systems, which are independent of the system under investigation, in order to further understand the unpredictable behavior exhibited by quantum systems. Investigations into classical chaos have also been conducted in order to better understand its effects on its quantum counterpart. Studies into both fields have highlighted remarkable behavior that has profound implications for both classical and quantum mechanics, as well as solid-state physics and quantum information technology.
- Investigating the Possibility of Free Will and Consciousness: The connection between chaos theory and free will is not clear-cut. Some authors argue that quantum mechanics does not have a connection to consciousness or free will, and Smart suggested that the brain remains deterministic due to quantum effects being insignificant on large numbers of molecules. However, chaos theory suggests that small inputs can be amplified, which could potentially influence decision-making in chaotic dynamical states in the brain. This has not been proven in practice yet, but it implies that quantum effects may play a role in allowing for free will if small disturbances can indeed have an amplified effect. Additionally, chaos theory reinforces the idea of indeterminism by demonstrating how complex systems are unpredictable and chaotic. As such, it can help explain how humans may be capable of making choices with some randomness involved.
- Analyzing the Impact of Human and Divine Action in a Nonlinear World: Analyzing the impact of human and divine action using chaos theory can help to solve everyday problems by providing insight into how unpredictable events may interact with each other. This knowledge could, for example, be used to anticipate when intervention may be necessary or when a problem might arise that was previously unforeseen. Additionally, understanding the possible outcomes of seemingly chaotic events can help establish preventative strategies before issues arise. By using chaos theory to understand and explain complex behavior, it is possible to develop solutions that take into account both human and divine influences.
- Examining the Implications of Realism and Chaos: Realism and chaos have important implications for how we view the world. Realism suggests that mathematical models accurately capture the behavior of target systems, while chaos implies that small changes in initial conditions can lead to large variations in the final outcome. These implications can impact how individuals think and behave as they consider complex systems, such as those found in nature or studied with time series data sets. Understanding realism and chaos is essential for making informed decisions when presented with dynamic phenomena.
- Exploring the Role of Nobel Prize-Winning Economic Theories: Chaos theory can be applied to the field of economics in order to better understand how markets work and how businesses can respond to changes. Chaos theory has been employed in a mixed fashion due to its complexity, but it can be used to help identify patterns that may not be evident in traditional economic models. It can also help predict changes in the stock market, as well as model the behavior of stock markets. Additionally, chaos theory is often used to observe positive feedback loops and negative feedback loops which have an impact on the economy's behavior - with positive feedback leading to exponential growth and negative feedback leading ultimately leading to collapse. Finally, chaos theory has been applied particularly successfully within the service industry due largely to its chaotic nature.
- Examining the Impact of Pentagon Office Culture on Modern Problems: Office culture has a significant impact on the way in which people approach and solve problems. It can limit individuals' creativity by denying them their agency, as well as suppressing diversity in the workplace. It is possible for office culture to create a barrier between employees and supervisors that prevents effective collaboration when trying to solve complex issues. Therefore, it is important for organizations to ensure that their office cultures are conducive to problem-solving and collaboration among staff members.
How does chaos theory help us understand complex systems better?
Chaos theory helps us understand complex systems better by illustrating how small changes to initial conditions can lead to unpredictable outcomes. It reveals the underlying order of these systems and can be used to study them, helping us predict their behavior in the future. Lorenz's findings were initially controversial but have since been proven through repeated experimentation.
What are the main principles of the Chaos Theory?
The main principles of Chaos Theory focus on understanding the behavior of complex systems and suggest that they should be maintained at the edge of chaos. This is done by studying a system's non-linearity and unpredictability, taking into account key terms such as the butterfly effect, attractor, and strange attractor. The Chaos Theory suggests that the destiny of the universe may be oriented toward complexity.
What are the applications of the Chaos Theory?
The Chaos Theory has applications in many fields, such as IT, modeling and predicting the behavior of complex systems, understanding how systems change over time, and how they are sensitive to small changes. Lorenz's experiment showed that even slight changes in input can cause large differences in output, revealing the importance of initial conditions when dealing with complex systems. The Chaos Theory is also used to understand how small changes can have large consequences in complex systems.
What is the Butterfly Effect in Chaos Theory?
The Butterfly Effect is a term used in Chaos Theory to describe the idea that very small variations in initial conditions can have large and unpredictable consequences. This concept was popularized by Edward Lorenz's computer models, which were able to accurately predict weather patterns a few minutes in advance. His model demonstrated how small errors could grow exponentially over time, resulting in huge differences between predictions. The Butterfly Effect is often referred to when discussing the events from Jurassic Park, as it illustrates how small changes can significantly alter the final outcome of events.
What is the Logistic Map?
The Logistic Map is a mathematical model used to describe the behavior of populations in which the number of subjects (x) changes over time. By illustrating the relationship between population size, food availability, and nutrition, as well as providing a means to predict long-term situations with scarce food availability, the Logistic Map provides an important tool for understanding chaos theory and its implications in mathematics.
What is the Mandelbrot Set?
The Mandelbrot Set has been of great significance to mathematicians due to its ability to generate new and interesting patterns. Its exploration has also aided in the study of chaos theory and the behavior of systems over time. Furthermore, it has served as an aesthetically pleasing subject for fractal art.
What is the Lyapunov Exponent?
The significance of the Lyapunov Exponent is that it can help model systems more accurately and predict their behavior over time. It provides information-theoretic insights that allow for small changes in an initial condition to have large consequences, enabling models to study sensitive initial conditions. The Lyapunov Exponent also helps assess the rate of divergence between two trajectories in phase space, while also being related to measure-theoretical mixing and properties of a K-system.
What is the Chaos Theory in Physics?
The Chaos Theory is a branch of physics that deals with the unpredictability and chaos of systems. It relates to the book because it offers a way to look at reality that is different from traditional models and can help explain how seemingly random events can lead to complex outcomes. The Feigenbaum constant is the number that controls the transition from order to chaos in systems, showing us that nature is far more complex than we had ever imagined. The Chaos Theory has applicability in many different fields, as it explains why complex systems like weather patterns or financial markets behave in unpredictable ways and often appear unrelated.
See Also
Predictive Analytics
Predictive Modeling