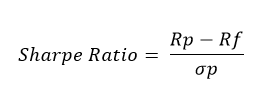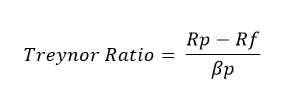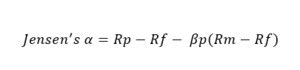Risk-Adjusted Return
Risk-adjusted return defines an investment's return by measuring how much risk is involved in producing that return, which is generally expressed as a number or rating. Risk-adjusted returns are applied to individual securities, investment funds and portfolios. Risk-adjusted returns can have a severe impact on portfolios. In strong markets, a fund with lower risk than the benchmark can limit returns, and a fund that entertains more risk than the benchmark may experience more sizable returns. It has been shown that, while losses may accrue in higher-risk funds during volatile periods, funds with a greater appetite for risk are more likely to outperform their benchmarks over full market cycles. [1]
Risk Adjusted Return Calculation Methods
Methods of Calculating Risk Ddjusted Return[2]
There are mainly 6 most widely-used methods of calculating risk adjusted return.
*Sharp Ratio: The Sharpe ratio symbolizes how well the return of an asset compensates the investor for the risk taken. When comparing two assets against a common benchmark, the one with a higher Sharpe ratio provides better return for the same risk (or, equivalently, the same return for lower risk). Developed by Nobel Prize winner, William F. Sharpe in 1966, Sharpe ratio is defined as the average return earned in excess of the risk-free rate per unit of volatility or total risk i.e standard deviation. The Sharpe ratio has become the most widely used method for calculating risk-adjusted return, however, it can only be accurate if the data has a normal distribution.
Risk Adjusted Return - Sharpe Ratio Rp = Expected Portfolio Return Rf – Risk Free Rate Sigma(p) = Portfolio Standard Deviation The Sharpe ratio can also help determine whether a security’s excess returns are a result of prudent investment decisions or just too much risk. Even as one fund or security can reap higher returns than its counterparts, the investment can be considered good if those higher returns are free from an element of additional risk. The more the Sharpe ratio, the better is its risk adjusted performance.
*Treynor Ratio: Treynor, is a measurement of the returns earned in excess of that which could have been earned on an investment that has no diversifiable risk. In short, it is also a reward-volatility ratio, just like the Sharpe’s ratio, but with just one difference. It uses a beta coefficient in place of standard deviations.
Risk Adjusted Return - Treynor Ratio Rp = Expected Portfolio Return Rf – Risk Free Rate Beta(p) = Portfolio Beta This ratio developed by Jack L. Treynor determines how successful an investment is in providing investors compensation, with consideration for the investment’s inherent level of risk. The Treynor ratio depends upon beta – which depicts the sensitivity of an investment to movements in the market – to evaluate the risk. The Treynor ratio is based on the premise that risk an integral element of the entire market (as represented by beta) must be fined, because diversification cannot eliminate it.
When the value of the Treynor ratio is high, it is a sign that an investor has generated high returns on each of the market risks he has assumed. The Treynor ratio helps one to understand how each investment within a portfolio is performing. This way, the investor also gains an idea as to how efficiently capital is being utilised.
*Jensen's Alpha: Alpha is often considered the active return on an investment. It determines the performance of an investment against a market index used as a benchmark, as they are often considered to represent the market’s movement as a whole. The excess returns of a fund as compared to the return of a benchmark index is the fund’s alpha. Basically, the alpha coefficient indicates how an investment has performed after accounting for the risk it involved:
Risk Adjusted Return - Jensens Alpha Rp = Expected Portfolio Return Rf – Risk Free Rate Beta(p) = Portfolio Beta Rm = Market Return Alpha<0: the investment has earned too little for its risk (or, was too risky for the return)
Alpha=0: the investment has earned a return adequate for the risk taken
Alpha>0: the investment has a return in excess of the reward for the assumed risk
*R-Squared: R-squared is a statistical measure that represents the percentage of a fund or security’s movements that is based on the movements in a benchmark index.
R-squared values range from 0 to 1 and are commonly stated as percentages from 0 to 100%. An R-squared of 100% means all movements of a security can be completely justified by movements in the index. A high R-squared, between 85% and 100%, indicates the fund’s performance patterns reflect that of the index. However, strong outperformance coupled with a very low R-Squared ratio will mean more analysis is required to identify the reason of outperformance.
*Sortino Ratio: Sortino ratio is a variation of the Sharpe ratio. Sortino takes the portfolio’s return and divides this by the portfolio’s “Downside risk” Downside risk is the volatility of returns below a specified level, usually the portfolio’s average return or returns below zero. Sortino shows the ratio of return generated “per unit of downside risk”.
Standard deviation includes both the upward as well as the downward volatility. However, most investors are primarily concerned about the downward volatility. Therefore, Sortino ratio depicts a more realistic measure of the downside risk embedded in the fund or the stock.
Risk Adjusted Return - Sortino Ratio Rp = Expected Portfolio Return Rf – Risk Free Rate Sigma(d) = Standard Deviation of Negative Asset Returns
*Modigliani Risk Adjusted Performance: Also known as Modigliani-Modigliani measure or M2, it is used for arriving at the risk adjusted return of an investment portfolio. It is used for measuring the return from a portfolio adjusted for the risk of the fund/portfolio relative to that of a benchmark (e.g. a specific market or index). It has taken its share of inspiration from the widely accepted Sharpe Ratio, however, has the significant advantage of being in units of percent return, which makes it easier to interpret.
M2 = Rp – Rm
Rp is the return on the adjusted portfolio Rm is return on the market portfolio The adjusted portfolio is the portfolio under management to be adjusted in such a way that it has the total risk as the market portfolio. The adjusted portfolio is constructed as a combination to the managed portfolio and risk-free asset where weights are assigned according to the risk borne.
The Importance of Risk-Adjusted Return
Why Risk Adjusted Return Matters[3]
The usefulness of the risk-adjusted return concept is that we can use it to evaluate a proposed strategy to determine whether it has historically been a better way to increase returns (or reduce risk) than simply adjusting any of several other well known variables (e.g., stock vs. bond allocation, duration of bond holdings, credit quality of bond holdings, etc.).
For example, imagine that you currently have a 50% stock, 50% bond portfolio that uses simple “total market” index funds for both the stock and bond portions. But then you meet with a financial advisor who suggests that you would be better off if you got rid of your total market stock funds and switched to a portfolio of individual stocks, picked according to a specific set of criteria. And this advisor shows you historical data demonstrating that his hand-picked stock portfolio has had higher returns over the last several years than your total market stock funds.
Obviously, one problem here is the critically dubious implication that the past is a good predictor of the future. But let’s set that aside for the moment to focus on another problem: A portfolio comprised of a handful of individual stocks will generally have far more risk than a broadly diversified total market stock portfolio.
Retail Investors and investment advisers who are swayed by strong recent investment performance could risk falling foul of a number of behavioural traps. Consider the chart below:
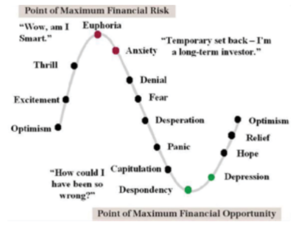
Source: WhiteChurch
See Also
Assessment of Risk
Framework for Risk Assessment
Risk Based Testing
Risk IT Framework
Risk Management
Risk Management Framework (RMF)
Risk Matrix
Risk Maturity
Risk Maturity Model (RMM)
Compliance
Corporate Governance of Information Technology (IT Governance)
Key Risk Indicator (KRI)
Business Continuity
Business Continuity Planning (BCP)
Disaster Recovery Planning
Enterprise Risk Management (ERM)
Crisis Management
Risk Analysis
Risk Mitigation
Risk-Adjusted Return on Capital (RAROC)
Own Risk and Solvency Assessment (ORSA)
References
- ↑ Defining Risk-Adjusted Return Investopedia
- ↑ What are the methods of calculating risk adjusted return? Wall Street Mojo
- ↑ Why Risk Adjusted Return Matters Mike Piper